Measurements take the guesswork out of everyday questions. Want to know how hot it is? Consult a thermometer. Need to know if that new bookcase will fit in your living room? Bust out the tape measure. Thermometers, tape measures, scales, radar guns, GPS receivers—they all interact in some way with the world around us and assign values to its properties.
In the quantum world, the purpose of measurement is the same. It’s about observing an object to learn about its properties. For something quantum, such as an atom or a photon, this can be a familiar property, like position, but it can also be something purely quantum, like spin.
So what’s different about quantum measurements? In short, the values of quantum properties simply don’t exist until they are measured.
That’s not to say that we don’t know the possible results of a quantum measurement ahead of time. We do. We just can’t say which one of those possible results we’ll get before we make the measurement.
This is very strange. To illustrate just how strange, first consider something that’s definitely not quantum, like a brick. Further, imagine that our humble brick is decked out with a GPS unit.
Prior to powering up the GPS, there’s no reason to doubt that the brick actually has a particular position. When it’s turned on, the GPS unit merely uncovers a value that is out there in the world, waiting to be measured. The same could be said of the brick’s speed, mass, density and anything else we might want to know about it.
This might seem obvious, but it exposes a deep truth about the everyday world: In principle, with enough information, it’s possible to perfectly predict the results of measurements before they are made.
But the same reasoning doesn't apply in the quantum realm. Instead of uncovering a value that existed before, quantum measurements themselves appear to create the value. It's not possible, even in principle, to perfectly predict the result of a single quantum measurement—an impossibility that scientists call "quantum indeterminacy."
At first glance, a coin flip may seem like an example of this kind of indeterminacy, but its uncertainty has nothing to do with quantum physics. An ordinary coin is definitely heads or tails under your hand after a flip; we just don’t know which one until we peek at it. If we are very careful to control for the gusto of our flip, to arrange the air currents just so, and to account for the microscopic bumps on the coin, we could keep track of how the coin rotates, bounces and lands. With perfect information, we could conceivably know the result of the flip without looking at the coin.
But even with perfect information, we can’t say whether a quantum coin was heads or tails before we measure it. Its indeterminacy is more fundamental than an ordinary coin and can stretch to properties and situations that we find hard to imagine—like the indeterminate position of an electron held in a superposition of both over here and over there.
A coin flip does share some similarities with quantum measurements. For instance, a coin has a 50-50 chance of coming up heads or tails. Quantum measurements also have chance outcomes, and different results occur with different probabilities.
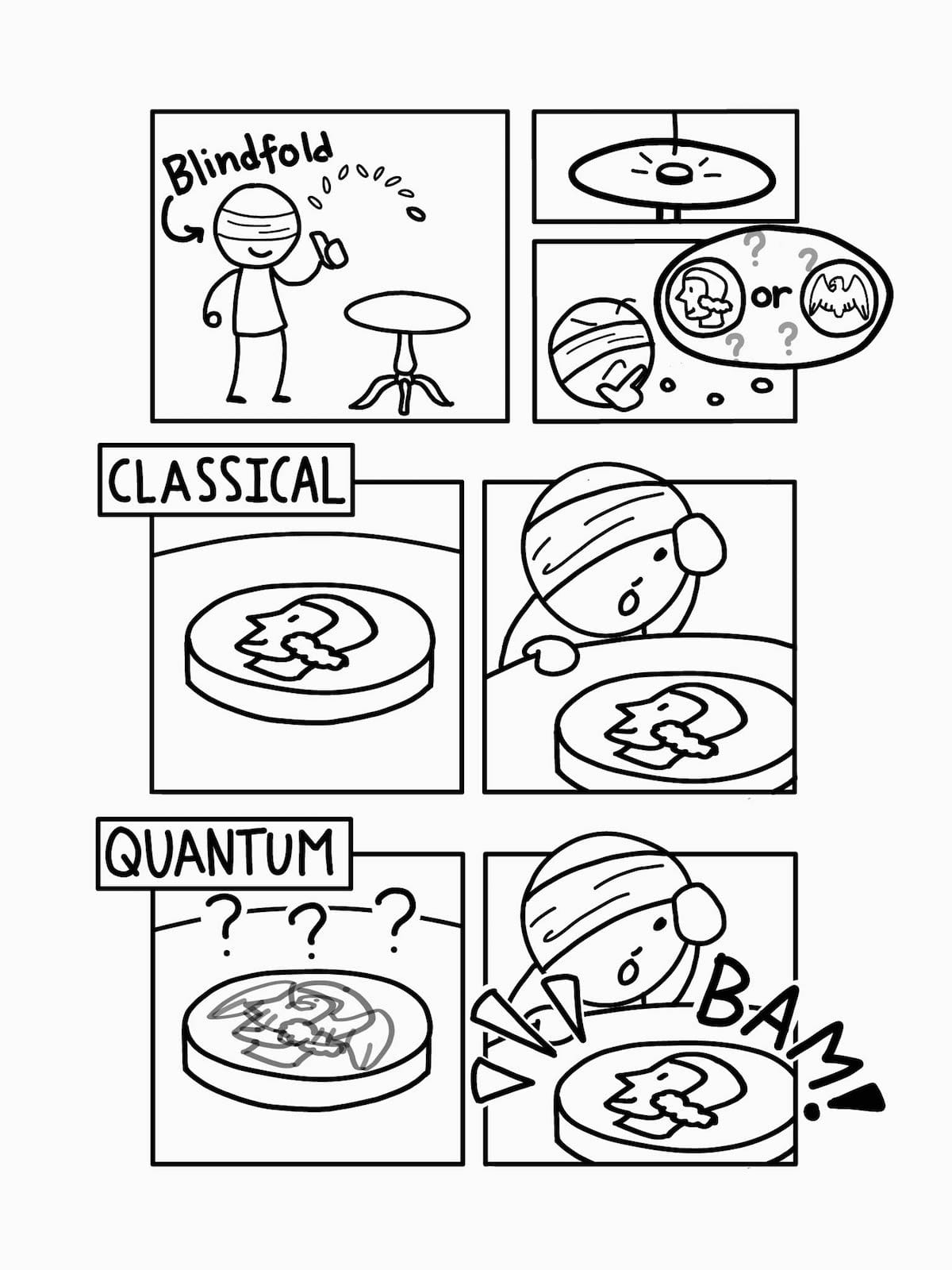
Furthermore, after a single coin flip, the 50-50 split collapses when you look at the coin and learn the outcome. Similarly, once you make a quantum measurement, you’re left with just one of the possible results—a situation that is often called "
Measurement is one of the most counterintuitive aspects of the quantum world, and it is intimately linked with an uncertainty that is inherent to all quantum systems. The idea of indeterminacy even led some early critics of quantum physics to proclaim the theory incomplete. Today, a debate about the meaning of quantum indeterminacy is still going on among physicists and philosophers who study the foundations of quantum physics.


