The Uncertainty Principle
Way down at the quantum scale, one thing you can be absolutely sure of is uncertainty.

One of the bedrock tenets of quantum physics is the uncertainty principle, formulated by Werner Heisenberg in the 1920s. It says that certain pairs of quantum properties—such as position (X) and momentum (P)---always maintain a careful balance. The more precisely you specify one, the less certain you are about the other.
This principle locks some quantum properties into a rigid trade-off reminiscent of a seesaw. On a playground, one seesaw rider can enjoy the view only when the other rider sits near the ground. Similarly, in the quantum world, to know where an
One can never know with perfect accuracy both of those two important factors which determine the movement of one of the smallest particles—its position and its velocity. It is impossible to determine accurately both the position and the direction and speed of a particle at the same instant.
Heisenberg originally applied the uncertainty principle to position and momentum, but there are others properties that obey its signature trade-off.
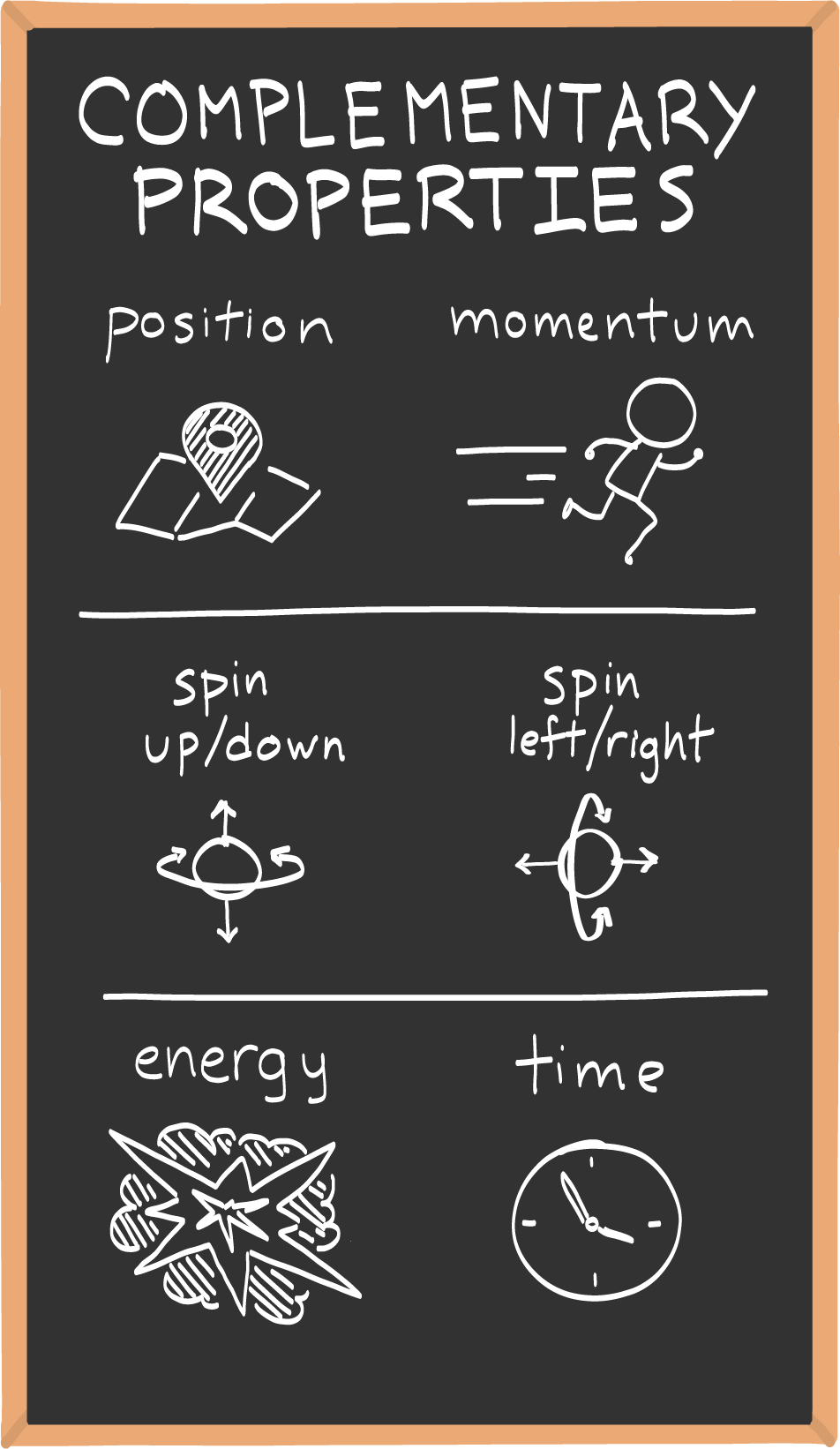
In the pantheon of quantum phenomena, the uncertainty principle can be a little hard to pin down. That’s because it’s not the only place in the quantum world where “uncertainty” rears its head. For example, the results of quantum measurements are uncertain before they’re made, but that’s not because of the uncertainty principle. Rather, it’s because quantum particles generally live in a superposition of different possibilities. At the time of measurement the superposition collapses into one of these possibilities at random.
The "uncertainty" in the uncertainty principle relates two different complementary properties that cannot be precisely known at the same time. One way to think about how those properties are related (besides the seesaw) is by considering the area of a rectangle.
If the width of the rectangle stands for the uncertainty in position and the height of the rectangle stands for the uncertainty in momentum, then the uncertainty principle says that the area of a rectangle can’t get any smaller than a certain number, related to a fundamental constant of nature. This is like saying that the acreage of your yard is fixed but the actual shape of it, narrow or wide, is flexible.
This fact—that the uncertainty principle constrains the product of two numbers—means that it contains a bit of wiggle room. The rectangle can get as skinny as you like in one direction, as long as the other direction grows to keep the area in check. Scientists use this idea—called squeezing because the shape ends up looking, well, squeezed—to enhance their ability to make high-precision measurements in the lab.
Crucially, the uncertainty principle is not a limit on the quality of such measurements. In general, it’s possible to measure the value of a single quantum property as accurately as you’d like, assuming you have the right tool. You just won’t be able to have the same confidence in another, complementary property at the same time.


